Dispersion in Statistics – Comprehensive Guide

• In this article you will get
• Introduction
• Definition of Statistics Dispersion
• Estimates of Dispersion
• Dispersion Measures and their types
• Calculating Dispersion
• Conclusion

Introduction

Statistics cannot be adequately explained by fundamental tendency measures. The suggestion between two statistics units will be the same even though they may differ. Therefore, one needs to comprehend the amount of variability in order to explain statistics. The dispersion measures are used to help provide this. Three often used metrics of dispersion are range, interquartile variety, and general deviation.

Definition of Statistics Dispersion

In statistics, the term “dispersion” refers to how dispersed a set of data is. Data that is distributed, stretched, or spread out among various categories is said to be in a condition of dispersion. Finding the magnitude of the distribution values that are predicted from the collection of data for the particular variable entails doing so. In statistics, the term “dispersion” refers to numerical data that is likely to change in any situation where the average value assumption is made.

The classification of the dataset into its own distinct dispersion criteria, such as variance, standard deviation, and range, in statistics facilitates the understanding of the dataset.

A collection of metrics called dispersion makes it possible to evaluate the caliber of data in a quantitatively objective way. Most data science courses begin with the fundamentals of statistics, and one such subject that you cannot afford to overlook is dispersion.

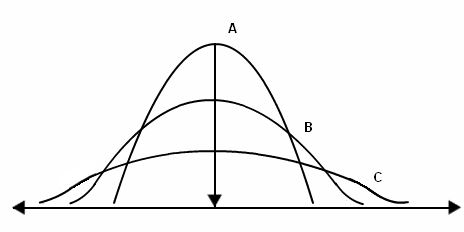
Estimates of Dispersion

Nearly the same unit is used in the dispersion measurements as in the quantity being measured. There are numerous measures of dispersion that we can use to gain deeper understanding of the data, including:

• Standard Deviation
• Skewness
• Range

Dispersion Measures and their types

Two basic categories of the Measure of Dispersion in Statistics provide strategies to gauge how diversely distributed the data is. In biological statistics, it is mostly employed. By determining whether or not they include units, we can quickly categorize them.

As a result, we can categorize the data into the following two groups:

• Measures of Absolute Dispersion
• Relative Dispersion Measures

Measures of Absolute Dispersion:

Absolute Measures of Dispersion is a measure of dispersion that has units; it uses the same unit as the initial dataset. The standard or mean deviation are two examples of the dispersion quantities used to indicate the absolute measure of dispersion. Rupees, centimeters, marks, kilogrammes, and other amounts that are measured according to the circumstance can all be used to describe the absolute measure of dispersion.

Types of Absolute Dispersion measures in statistics:

Range:The difference between the highest and smallest value of the data variability is measured by range. The most basic measure of dispersion is the range.The average of the values is used to generate the term “mean” (). Add all the results together, then divide the result by the total number of words to obtain the Mean.

Variance (2):The variance is easily computed by adding up the squared distances between each term in the distribution and the mean, dividing by the sum of those squared distances, and multiplying the result by the total number of terms in the distribution.

Standard Deviation:The square root of Variance is a common way to visualize standard deviation. Any data must first have a variance before the standard deviation can be calculated. The ideal way to measure dispersion is using standard deviation.

Mean deviation:Also referred to as an average deviation, mean deviation can be calculated using the mean or median of the data. A different item that follows the central tendency is used to depict mean deviation as its arithmetic deviation.

Relative Dispersion Measures:

In statistics, the values without units represent the relative measure of dispersion. To compare the distribution of two or more datasets, a relative measure of dispersion is employed.

The only distinction between the Relative Measure of Dispersion and the Absolute Measure of Dispersion is the quantity used for measurement.

Types of Relative Measure of Dispersion: Relative Measure of Dispersion is the calculation of the coefficient of Dispersion when two series that have significantly different averages are compared.

When comparing two series using various measurement units, the coefficient of dispersion is most frequently used.

1.Coefficient of Range:This statistic is determined by dividing the difference between the distribution’s largest and smallest terms by the sum of those terms.

Formula:

2.Coefficient of Variation:The coefficient of variation is used to compare the homogeneity or consistency of the two sets of data.

Formula:

3.Standard deviation coefficient:The standard deviation coefficient is the ratio of the standard deviation to the mean of the term distribution.

Formula:

4.Coefficient of quartile deviation:The ratio of the difference between the upper and lower quartiles to the total of the upper and lower quartiles is known as the coefficient of quartile deviation.

Formula:

5.Coefficient of Mean Deviation:Using the data’s mean or median, the coefficient of mean deviation can be calculated.

When using Python with data science, this is made easier because the programming language provides a variety of statistical packages for this. These formulae are very useful when calculating various elements of data.

Why statistics should consider dispersion?

Grasp of statistics requires an understanding of dispersion. Understanding ideas like the diversification of the data, how the data is distributed, how it is preserved, and how the data is kept over the core value or central tendency is beneficial.In addition, statistics’ dispersion offers us a technique to learn more about the distribution of data.

For illustration,The Mean, Median, or Range of 3 independent samples may be the same, yet their levels of variability may be entirely different.

Calculating Dispersion

The many dispersion measures that are mentioned in the various types of Measures of Dispersion discussed above can be used to calculate dispersion with ease. It is crucial to comprehend the changes in words and usage before measuring the data.

The dispersion can be calculated using the method listed below:

• Typical standard deviation
• Variance
• Marginal deviation

Statistical dispersion representation:

Pie charts and graphs are two common ways to display dispersion in statistics. Some of the various techniques employed include:

• Box plots
• Stem plots
• Leaf plots
• Dot plots

Example: The values 3,8,6,10,12,9,11,10,12,7, what is their variance?The formula below can be used to determine how the values have varied:

What is a prime instance of dispersion?

A non-statistical example of dispersion is the rainbow, which is made up of white light that is divided into seven distinct colors by wavelengths.

It can be measured statistically in the following ways:

• Average standard deviation
• Standard deviation of the mean
• Average absolute deviation
• Interquartile variation
• Typical deviation

Conclusion

In statistics, dispersion is a measure of how variable some data or words are. Where some of the instrumental measurements are determined to be inaccurate, such variability may result in random measurement mistakes.

It is a statistical method of expressing how the terms are distributed throughout the various data sets. The data is always found to be more dispersed the more sets of values there are. The values in this range can range from 5 to 10 to 1000 to 10,000. The range of descriptive statistics provides a description of this distribution of data. Dot plots, box plots, and other visual representations of statistics’ measures of dispersion are available. Learn about dispersion and other statistical concepts in the knowledgehut program’s beginning Python with Data Science course.