Free Float Vs Total Float

Free Float Vs Total Float

Total floats and free floats have an important role in the development of a network diagram. A better understanding of these terms will help you draw a network diagram and analyze a critical path.

Total Float

Float is also known as total float.

Total float is how long an activity can be delayed, without delaying the project completion date. On a critical path, the total float is zero.

Total float is often known as the slack.

You can calculate the total float by subtracting the Early Start date of an activity from its Late Start date.

Total Float = Late Start date – Early Start date

Or 

You can get it by subtracting the activity’s Early Finish date from its Late Finish date. 

Total Float = Late Finish date – Early Finish date

Free Float

Free float is how long an activity can be delayed, without delaying the Early Start of its successor activity.

You can calculate the free float by subtracting the Early Finish date of the activity from the Early Start date of the next.

Free Float = ES of next Activity – EF of current Activity

Please note that if two activities are converging into a single activity, only one of these two activities may have a free float.

Example: 1

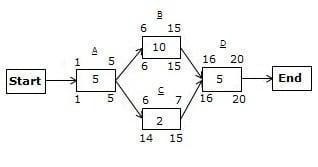
In the above network diagram, you can see two paths:

1. 1. The first path is A->B->D with a 20-day duration.
2. 2. The second path is A->C->D with a 12-day duration.

The path A->B->D is the critical path because it has the longest duration.

Calculating the Total Float

The path A->B->D is a critical path; therefore, it will not have a total float.

The path A->C->D is a non-critical path, so it can have a total float.

There are two methods to calculate the total float. In the first, you subtract the duration of the non-critical path from the critical path.

In the second method, you find the total float for any activity by subtracting the Early Start date from the Late Start date (LS – ES) or subtracting the Early Finish date from the Late Finish date (LF – EF) on any activity.

The first method of finding the total float

Total float = duration of the critical path – duration of the non-critical path

= (duration of the path A->B->D) – (duration of the path A->C->D)

= 20 – 12

= 8

Hence, the total float is eight days.

The second method of finding the total float

On the path A->C->D, Activity A and D lie on the critical path; therefore, they will not have a total float. Only Activity C can have a total float.

We can calculate the total float by using either the finish dates or start dates. I will show you both ways to find it.

First, we will go with the Late Finish and Early Finish dates:

Total float for Activity C = (LF of Activity C – EF of Activity C)

= 15 – 7

= 8

Now, the second formula:

Total float for Activity C = (LS of Activity C – ES of Activity C)

= 14 – 6

= 8

The durations are the same. This means that both formulas will give you the same result.

Calculating the Free Float

From the figure, you can see that only Activity C can have a free float because all other activities are on the critical path.

Let’s find it.

Free float of Activity C = ES of next activity – EF of Activity C – 1

= 16 – 7 – 1

= 8

Hence, the free float for Activity C is eight days.

Now we will discuss a more complex example.

Example: 2

For the below-given network diagram, find which activities can have a free float and calculate the free and total float, considering the duration in days.

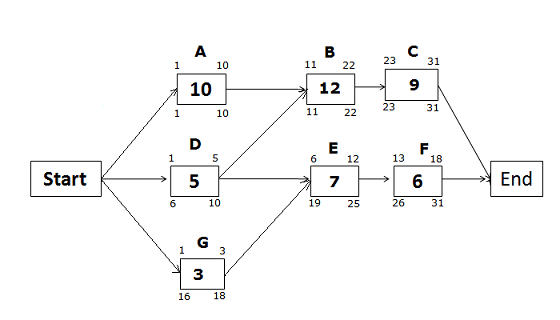
We know that:

Free float = ES of next activity – EF of current activity – 1

In the above diagram, Activity G can have the free float because Activity D and G converge on one common activity.

Activity D will not have a free float because its successor, Activity E, is starting the day after the completion of Activity D.

Free Float for Activity G

We know the formula for free float:

Free float of Activity G = Early Start of Activity E – Early Finish of Activity G – 1

= 6 – 3 – 1

= 2

Total Float for Activity G

Total float for Activity G = Late Finish of Activity G – Early Finish of Activity G

= 18 – 3

= 15

You can see here that the free float for Activity G is two days, and the total float is fifteen days. Both are different.

Critical Path Method Calculation Example

Let us understand the floats with the help of a small example. Refer to the following network diagram. It is solved using 1 method.

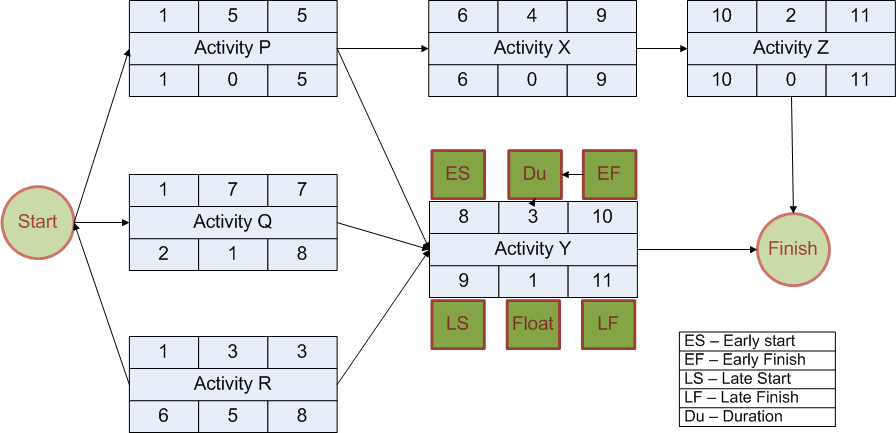
As per the above diagram:

• There are 6 activities viz. P, Q, R, X, Y, and Z.
• P, Q, and R start as soon as the project starts.
• X is the successor of P.
• Y is the successor of P, Q and R.
• Z is the successor of X.

Project Float is also referred to as Slack – some Project Management literature use the terms Total Slack and Free Slack. Some books just use ‘Float’ to refer to ‘Total Float’. In this article, I have used the Total Float (TF) and Free Float (FF).

Definition, Meaning And Formulae For Total Float

Total Float is the maximum amount of time an Activity can be delayed without delaying the Project.

e.g. if TF for an Activity Alpha is ‘n’ days, it means Activity Alpha can be delayed by ‘n’ days without impacting the Project Finish Date. Delaying Alpha may delay its successor but the finish date would remain the same.

You can refer to PMI’s Lexicon for a few other standard definitions.

The TF can be calculated by using either of the following formulas

TF = LF – EF

OR

TF = LS – ES

Both the formulas will produce the same result. e.g. In the above diagram TF for Activity P and Activity Q are 0 and 1 respectively.

Here are a few other pertinent points about TF:

• Buffer (Contingency Reserve) and TF are not the same. Buffer is purposefully introduced in an activity whereas TF is due to its placement in the Network Diagram.
• TF is calculated separately for each activity. TF is mentioned in the lower middle box of each activity in the above diagram.
• Some professionals feel that TF is a misnomer. It says ‘total’ but it is calculated for each activity and not for the entire path.
• TF is shared among the activities that are on the same path in a Network Diagram. If one activity uses TF, the TF of other activities will proportionately reduce. e.g. If Q uses 1 unit of TF on Path QY, then Y will have n0 TF.
• The activities on the Critical Path have the least amount of TF. Generally it is zero but it could be negative also. In the above diagram, PXZ is the Critical Path.

Definition, Meaning And Formulae For Free Float

Free Float is the amount of time an Activity can be delayed without impacting the Early Start date of any of its Immediate Successors.

You can refer to Max Wideman’s Glossary for a few other standard definitions.

e.g. Consider Activity Alpha & Activity Beta that have a Finish to Start relationship between them. Activity Beta is successor to Activity Alpha. If Activity Alpha has a FF of ‘n’ days, it means Activity Alpha can be delayed by ‘n’ days without impacting the Early Start of Activity Beta.

FF can be calculated by using one of the following formulas.

FF = min(ES of Successors) – (ES of Activity in Question) – (Duration of Activity in Question)

OR

FF = min(ES of Successors) – (EF of Activity in Question)

The first formula is a generic formula and will work for both o and 1 method in critical path analysis but the second one will work only if you have used 1 method.

Refer to the above network diagram again.

FF for Activity X is 0 as any delay in X will delay ES of Z.

FF Activity Q is 0 as any delay in Q will delay ES of Y. Notice that TF of Activity Q is 1.

FF Activity R is 4. The ES of Y will change only if R is delayed by more than 4 days. Notice that TF of Activity Q is 5.

Here are a few other pertinent points about FF:

• Lag and FF are not the same. Lag is purposefully introduced in an activity whereas FF is due to its placement in the Network Diagram.
• FF is calculated separately for each activity. FF is generally not mentioned in the Network Diagram.
• FF is useful when there is an imposed start date for a Successor activity.
• All the successor activities should be considered while calculating the FF.
• TF and FF of an Activity can be different.
• The above formula for FF is applicable for Finish to Start relationships only.