What is Dimensionality Reduction? : ( A Complete Guide with Best Practices )

• In this article you will get
• 1.What’s Dimensionality Reduction?
• 2.The Curse of Dimensionality
• 3.Benefits of applying Dimensionality Reduction
• 4.Disadvantages of dimensionality Reduction
• 5.Three styles are used for point selection
• 6.Common ways of Dimensionality Reduction
• 7.Conclusion

What’s Dimensionality Reduction?

The dataset contains a large number of input features in colorful cases, which further complicates the prophetic modeling task. Because training datasets with a large number of features are veritably delicate to visualize or prognosticate, for similar cases, dimensionality reduction ways need to be used.

Dimensional reduction ways can be defined as, “ It’s a system of converting a dataset of advanced confines to a dataset of lower confines which ensures that it provides invariant information.It’s generally used in fields that deal with high- dimensional data, similar as speech recognition, signal processing, bioinformatics, etc.

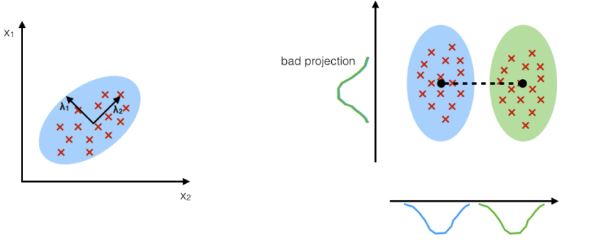
The Curse of Dimensionality

Handling high- dimensional data is veritably delicate in practice, which is generally known as the curse of dimensionality.As the number of features increases, the number of samples also increases proportionally, and the probability of overfitting also increases.However, it tends to overfit and affect in poor performance, If a machine literacy model is trained on high- dimensional data.Therefore, there’s frequently a need to reduce the number of features, which can be done with dimensionality reduction.

Benefits of applying Dimensionality Reduction

Some of the benefits of applying dimensionality reduction fashion to the given dataset are mentioned below:

• By reducing the confines of the features, the space needed to store the dataset is also reduced.
• Smaller confines of the features bear lower calculation training time.
• The reduced confines of the dataset’s features help to visualize the data snappily.
• It removes gratuitous features( if present) while taking care of multiplexing.

Disadvantages of dimensionality Reduction

There are also some disadvantages of enforcing dimensionality reduction, which are mentioned below:

In PCA dimensionality reduction ways, occasionally the top factors needed to be considered are unknown.

Approaches of Dimension Reduction:

Point selection is the process of opting a subset of applicable features and discarding inapplicable features present in the dataset to make a model of high delicacy. In other words, it’s a way of opting the optimal features from the input dataset.

Three styles are used for point selection

1.ludge styles

In this system, the dataset is filtered, and a subset containing only applicable features is taken. Some common ways of the sludge system are:

• Co – relationship
• Ki-square test
• Anova
• Information gain,etc.

2.Wrapper styles

The wrapper system has the same thing as the sludge system, but requires a machine literacy model to estimate.This system is more accurate than the filtering system but is more complicated to work with. Some common ways of wrapper styles are:

• Further selection
• Backward selection
• Bi-directional elimination

3.Bedded styles

Bedded styles examine different training duplications of the machine literacy model and estimate the significance of each point. Some common ways of Bedded styles are:

• Lasso.
• Elastic mesh.
• Ridge retrogression,etc.

Point birth:

Point birth is the process of converting a space of numerous confines into a space of lower confines. This approach is useful when we want to have complete information but use lower coffers while recycling the information.

Some common point birth ways are:

• Top element analysis
• Direct discriminant analysis
• Kernel PCA
• Quadratic discriminant analysis

Common ways of Dimensionality Reduction

Star element Analysis( PCA):

Star element analysis is a statistical procedure that converts an observation of identified features into a set of linearly identified features with the help of orthogonal metamorphoses. These recently converted characteristics are called top factors.

Backward point elimination:

The backward point elimination fashion is substantially used when developing direct retrogression or logistic retrogression models. The following ways are followed in this fashion in dimensionality reduction or point selection In this fashion, all n variables of the given dataset are first taken to train the model.

Now we will remove one point each time and train the model n times on n- 1 features, and calculate the performance of the model. We ’ll examine the variable that caused the lowest or no change in the model’s performance, and also we ’ll discard that variable or features; After that, we ’ll be left with n- 1 features.

Repeat the whole process until no point drops:

In this fashion, by opting for the optimal performance of the model and the maximum tolerable error rate, we can define the optimal number of features needed for the machine learning algorithm.

Forward point selection:

This means, in this fashion, we don’t exclude the trait; rather, we will find the stylish features that can make the loftiest increase in the performance of the model. The following ways are followed in this fashion. We start with just one point, and gradually we ’ll add each point one at a time.

Missing value rate:

Still, we discard those variables because they don’t contain important useful information. If a dataset has too many missing values. To do this, we can set a threshold position, and if a variable is missing values lesser than that threshold, we will discard that variable. The advanced the threshold value, the more effective the reduction.

Low Friction sludge:

analogous to the missing value rate fashion, a data column with many changes in the data contains lower information. Thus, we need to calculate the friction of each variable, and all data columns with friction lower than a given threshold are discarded because low friction features won’t affect the target variable.

Random timber:

Random timber is a popular and veritably useful point selection algorithm in machine literacy. This algorithm has an in- erected point significance package, so we don’t need to program it independently. In this fashion, we need to induce a large set of trees against the target variable, and with the help of operation statistics of each point, we need to find the subset of features.

Factor analysis:

A high correlation with each other, but they may be identified with variables in other groups. with low correlation. We can understand this with an illustration, like if we’ve two variables income and charges. These two variables have a high correlation, meaning that people with advanced inflows spend further, and vice versa.

bus- encoder:

One of the popular styles of dimensionality reduction is the bus- encoder, which is a type of ANN or artificial neural network, and its main purpose is to copy the inputs to their labors. In this, the input is compressed into a secret- space representation, and affair is produced using this representation. It substantially consists of two corridor.

Decoder The function of the decoder is to reconstruct the affair from the latent- space representation.

The significance of Dimensionality Reduction:

There are principally three reasons for dimensionality reduction

• Visualization
• Interpretability
• Time and space complexity

Let us understand this with an illustration:

Imagine we’ve worked on a MNIST dataset which has 28 × 28 images and when we convert the images into features we get 784 features.Still, how can we suppose 784 confines in our mind?

If we try to suppose each point as a dimension.We can not imagine the scattering of points of 784 confines. Let’s say you’re a data scientist and you have to explain your model to guests who do n’t understand machine literacy. How would you explain the working of 784 features or confines to them?

Dimensionality Reduction illustration:

Then’s an illustration of dimensionality reduction using the PCA system mentioned before. To do this, you produce a fine representation of each dispatch as a bag- of- words vector. For a single dispatch, each entry in the bag- of- words vector is the number of times the corresponding word appears in the dispatch( with a zero, meaning it does n’t appear at each).

Now suppose you have constructed a bag- of- words from each dispatch, which gives you a sample of bag- of- words vectors, X1 xm. still, the confines( words) of all your vectors aren’t useful for spam/ not for spam brackets. For illustration, words like “ credit, ” “ bargain, ” “ offer, ” and “ trade ” would be better campaigners for spam brackets than “ sky, ” “ shoe, ” or “ fish. Also sort the performing figures in descending order and choose the top eigenvalues of p. Your affair data is now a protuberance of the original data onto p eigenvectors. therefore, the estimated data dimension has been reduced top.

After calculating the low- dimensional PCA protrusions of your bag- of- words vector, you can use the protuberance with colorful bracket algorithms to classify emails rather than using the original dispatch. Estimates are lower than the original data, so effects move briskly.

Conclusion

In simple words, dimensionality reduction refers to reducing the confines or features so that we can gain a further explanatory model, and ameliorate the performance of the model.

An intuitive illustration of dimensionality reduction can be bandied through a simple dispatch bracket problem, where we need to classify whether a dispatch is spam or not. This can include a large number of features, such as whether thee-mail has a common title, the content of thee-mail, whether the dispatch uses a template, etc. still, some of these features may overlap. In another situation, a bracket problem that depends on both moisture and downfall can be added up in just one underpinning point, as both of the below are largely identified.

A 3- D bracket problem can be delicate to visualize, whereas a 2- D bone can be counter plotted to a simple 2- dimensional space and a 1- D problem to a simple line. The figure below illustrates this conception, where a 3- D point space is resolved into two 1- D point spaces, and latterly, if set up to be identified, the number of features is further reduced. could.