What is Logistic Regression?

What is Logistic Regression?

• Logistic regression is the appropriate regression analysis to conduct when the dependent variable is dichotomous (binary). 
• Like all regression analyses, the logistic regression is a predictive analysis.  Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables.
• Sometimes logistic regressions are difficult to interpret; the Intellectus Statistics tool easily allows you to conduct the analysis, then in plain English interprets the output.

Types of Logistic Regression:

1. Binary Logistic Regression:

The categorical response has only two 2 possible outcomes. 

E.g.: Spam or Not

2. Multinomial Logistic Regression:

Three or more categories without ordering. 

E.g.: Predicting which food is preferred more (Veg, Non-Veg, Vegan)

3. Ordinal Logistic Regression:

Three or more categories with ordering. 

E.g.: Movie rating from 1 to 5

Logistic regression predicts the probability of an outcome that can only have two values (i.e. a dichotomy). The prediction is based on the use of one or several predictors (numerical and categorical). A linear regression is not appropriate for predicting the value of a binary variable for two reasons:

• A linear regression will predict values outside the acceptable range (e.g. predicting probabilities outside the range 0 to 1)
• Since the dichotomous experiments can only have one of two possible values for each experiment, the residuals will not be normally distributed about the predicted line.

On the other hand, a logistic regression produces a logistic curve, which is limited to values between 0 and 1. Logistic regression is similar to a linear regression, but the curve is constructed using the natural logarithm of the “odds” of the target variable, rather than the probability. Moreover, the predictors do not have to be normally distributed or have equal variance in each group.

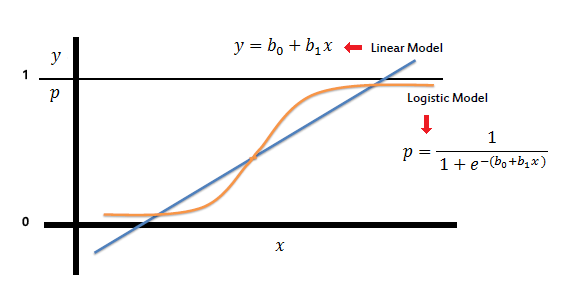
In the logistic regression the constant (b0) moves the curve left and right and the slope (b1) defines the steepness of the curve. By simple transformation, the logistic regression equation can be written in terms of an odds ratio.

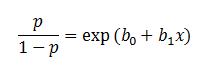
Finally, taking the natural log of both sides, we can write the equation in terms of log-odds (logit) which is a linear function of the predictors. The coefficient (b1) is the amount the logit (log-odds) changes with a one unit change in x.

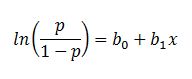
As mentioned before, logistic regression can handle any number of numerical and/or categorical variables.

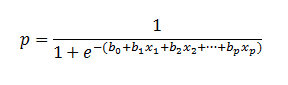
There are several analogies between linear regression and logistic regression. Just as ordinary least square regression is the method used to estimate coefficients for the best fit line in linear regression, logistic regression uses maximum likelihood estimation (MLE) to obtain the model coefficients that relate predictors to the target. After this initial function is estimated, the process is repeated until LL (Log Likelihood) does not change significantly.

Benefits of using regression analysis:

1. 1. It indicates the significant relationships between dependent variable and independent variable.
2. 2. It indicates the strength of impact of multiple independent variables on a dependent variable.

Advantages of logistic regression

• Logistic regression is much easier to implement than other methods, especially in the context of machine learning: A machine learning model can be described as a mathematical depiction of a real-world process. The process of setting up a machine learning model requires training and testing the model. Training is the process of finding patterns in the input data, so that the model can map a particular input (say, an image) to some kind of output, like a label. Logistic regression is easier to train and implement as compared to other methods.
   
• Logistic regression works well for cases where the dataset is linearly separable: A dataset is said to be linearly separable if it is possible to draw a straight line that can separate the two classes of data from each other. Logistic regression is used when your Y variable can take only two values, and  if the data is linearly separable, it is more efficient to classify it into two separate classes.
   
• Logistic regression provides useful insights: Logistic regression not only gives a measure of how relevant an independent variable is (i.e. the (coefficient size), but also tells us about the direction of the relationship (positive or negative). Two variables are said to have a positive association when an increase in the value of one variable also increases the value of the other variable. For example, the more hours you spend training, the better you become at a particular sport. However: It is important to be aware that correlation does not necessarily indicate causation! In other words, logistic regression may show you that there is a positive correlation between outdoor temperature and sales, but this doesn’t necessarily mean that sales are rising because of the temperature.